Réseaux - Sciences de l'ingénieur

1. Définition d'un système asservi

Un système asservi est un système automatique qui ajuste sa sortie pour suivre une consigne donnée, en minimisant l'écart entre la consigne et la sortie grâce à un retour d'information (feedback). Ce principe est utilisé dans de nombreuses applications : contrôle de température, pilotage automatique, robots, etc.

Exemple : Régulateur de température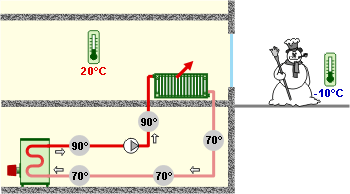

Consigne : Température souhaitée (par exemple, 22 °C).
Capteur : Mesure la température actuelle.
Actionneur : Chauffage ou refroidissement.
Correcteur : Compare la température mesurée à la consigne et ajuste le chauffage en conséquence.

2. Structure générale d’un système asservi

Schéma-bloc général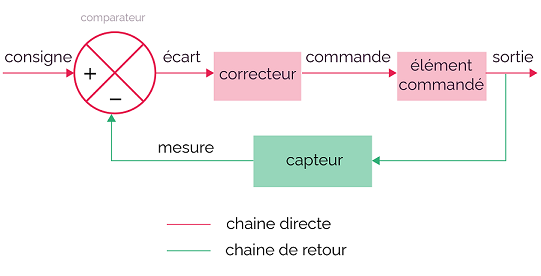

Consigne (r) : Valeur à atteindre.
Correcteur : Évalue l'erreur entre la consigne et la sortie.
Système : Partie physique à contrôler (moteur, chauffage, etc.).
Capteur : Retour d’information sur l’état du système.
Sortie (s) : Résultat effectif.

Un système asservi est caractérisé par sa fonction de transfert.
La fonction de transfert est un outil mathématique utilisé pour modéliser et analyser les systèmes dynamiques linéaires et invariants dans le temps (LTI). Elle relie la sortie d'un système à son entrée dans le domaine de Laplace.

la fonction de transfert F(p) est définie comme le rapport entre la transformée de Laplace de l'entrée E(p) et celle de la sortie S(p), en supposant des conditions initiales nulles :F(p)= S(p) / E(p) où :

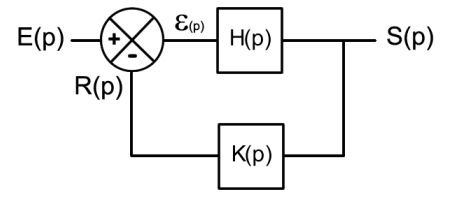
F(p) est la fonction de transfert.
S(p) est la transformée de Laplace de la sortie y(t).
E(p) est la transformée de Laplace de l'entrée r(t).
p est la variable complexe du domaine de Laplace (p=σ+jω).

On trouvera aussi le rapport suivant:

F(p)= H(p) / 1+K(p).H(p)
.

3. Types de systèmes

Les systèmes asservis peuvent être classés en ordre 0, ordre 1, ou ordre 2 en fonction de leur comportement dynamique.

3.1. Système d'ordre 0 (Gain pur)

Exemple : Amplificateur audio.

Fonction de transfert :H(p)=K (gain constant).
Réponse à une entrée échelon : Sortie instantanée proportionnelle à l'entrée.

Représentation graphique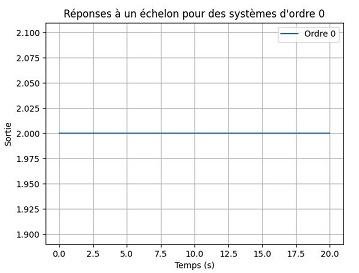

3.2. Système d'ordre 1 (Intégrateur)

Exemple : Chauffage (la température change progressivement).

Fonction de transfert : H(p)= K / τp+1
τ : Constante de temps (rapidité du système). Cela correspond au temps mis par le système pour atteindre 63% de sa valeur.

Réponse à un échelon : Croissance exponentielle vers une valeur finale.

Représentation graphique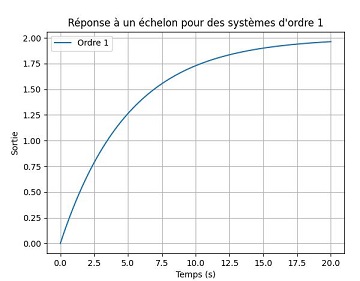

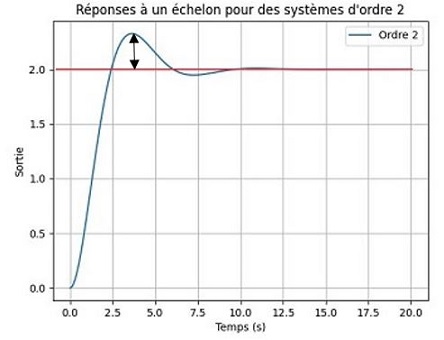
Système d'ordre 2 (Oscillations amorties)

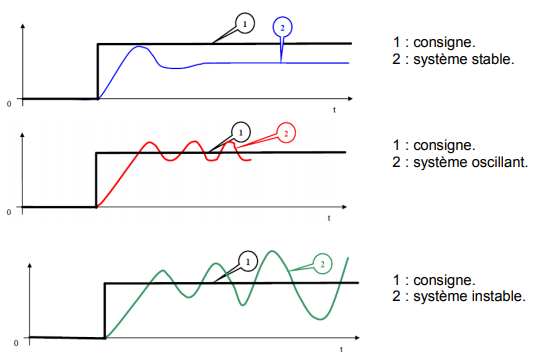
Exemple : Suspension de voiture. Fonction de transfert : H(p)= K / τ²p²+2ξτp+1
ξ : Coefficient d’amortissement.

Réponse :

ξ<1 : Oscillations amorties. Le système oscille autour de la consigne avec une amplitude qui décroît progressivement.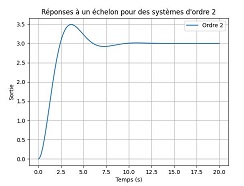
ξ=1 : Amortissement critique. Le système converge vers la consigne sans oscillations, mais le temps de réponse est minimal.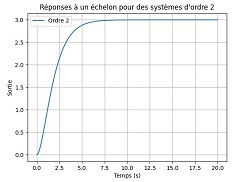
ξ>1 : Système sur-amorti. Le système converge lentement vers la consigne sans oscillations.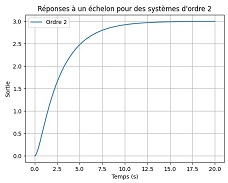
ξ=0 : Oscillations non amorties. Le système oscille indéfiniment autour de la consigne.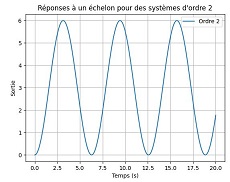
ξ≈0.7 : Réponse optimale pour un compromis entre rapidité et dépassement.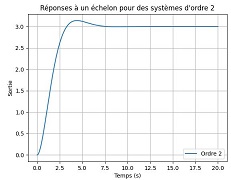

Exercice 1 : Identifier des systèmes de différents ordres.

On donne les fonctions de transfert suivantes :

Système A :H(p)=3
Système B :H(p)= 4 / 2p+1
Système C :H(p)= 5 / p²+3p+2

1. Identifier l’ordre de chaque système (0, 1 ou 2).

Système A: Système d'ordre 0 car pas de p au dénominateur
Système B: Système d'ordre 1 car dénominteur de degré 1
Système C: Système d'ordre 2 car dénominateur de degré2.

Analyse de la réponse temporelle

4.1. Paramètres caractéristiques

Un système asservi est caractérisé par :

La précision: C’est la capacité du système à se rapprocher le plus possible de la valeur de consigne.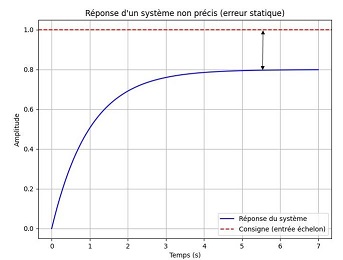

Pour déterminer la précision d'un système, on calcule l'erreur statique ε qui représente l'écart entre la consigne et la valeur finale atteinte par le système.
Elle se calcule de la façon suivante:

ε= consigne - valeur finale / consigne

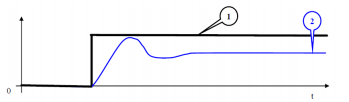
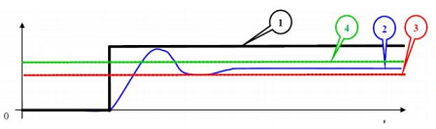
La rapidité : C’est la capacité du système à atteindre dans les meilleurs délais son régime stable. La rapidité d’un système est définie par son temps de réponse tr (plus tr est petit plus le système est dit rapide).
Dans l’exemple suivant, la courbe noire (1) représente la consigne et la bleue (2) représente la réponse du système. La valeur finale du système est nommée vf

Le temps de reponse: C'est le temps mis par le système pour atteindre sa valeur finale à + ou - 5%.

1. Consigne
2. Valeur finale du Système
3. Droite à 95% de la valeur finale
4. Droite à 105% de la valeur finale

Pour déterminer le temps de réponse d’un système :

On trace une droite à 95% de la valeur finale vf (3);
On trace ensuite une droite à 105% de la valeur finale vf (4).
On détermine le temps à partir duquel la courbe reste entre ces deux valeurs

La stabilité: Pour une consigne constante la sortie doit tendre vers une constante.

Le dépassement: Le dépassement se caractérise par l’amplitude de l’oscillation la plus grande.

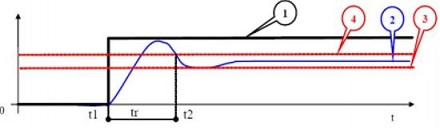
2. Les correcteurs

Un correcteur est un algorithme de calcul qui délivre un signal de commande à partir de la différence entre la consigne et la mesure. Le correcteur PID agit de 3 manières :

action Proportionnelle : amélioration de l’erreur statique mais provoque un dépassement plus important
action Intégrale : lorsque 1 / τ_i est présent l'erreur statique est annulée. Quand il augmente, la valeur finale est plus rapidement atteinte pour les systèmes présentant de grandes marges de stabilité. Le temps d'établissement en régime stationnaire s'allonge pour les autres systèmes qui vont davantage osciller.

action Dérivée : lorsque τ_d augmente, le temps de montée diminue (la réponse du système ainsi corrigé est plus rapide) et les dépassements sont mieux amortis. La stabilité est améliorée. N'agit pas sur la précision du système.

Exercice 2 : Ajout d'un correcteur proportionnel

On donne la fonction de transfert suivante :

Système B :H(p)= 2 / 5p+1
1. Identifier l’ordre du système (0, 1 ou 2).
2. Ajouter un correcteur proportionnel de gain K(p)=3 au système. La nouvelle fonction de transfert en boucle ouverte est donnée par :H_c(p) = K(p)*H(p) et simplifier.
3.Quel est l'effet du correcteur proportionnel?

1. Il s'agit d'un système d'ordre 1 car le dénominteur est de degré 1
2. En ajoutant un correcteur proportionnel K(p), on obtient:
H_c(p)= 2 X 3 / 5p+1 = 6 / 5p+1
3. Ce correcteur permet de réduire l'erreur statique

Exercice type bac: Etude d'un quadricoptère

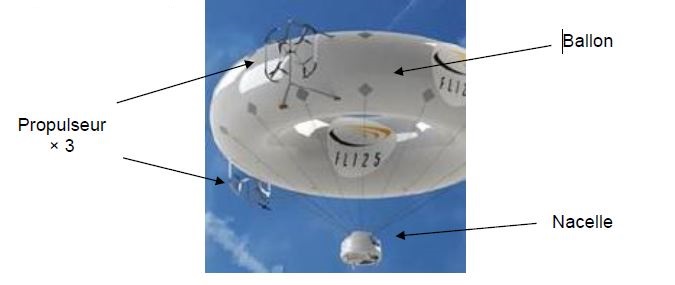
L'Aéronde est un concept innovant qui permet un mode de déplacement aérien électrique, à faible consommation. Ses fonctions principales sont de transporter une personne ou du matériel d'un point A à un point B.

L'Aéronde est un dirigeable avec un ballon de forme torique, gonflé à l'hélium (He) ou au dihydrogène (H2). L'Aéronde suit la même législation que les ULM car le pilote est embarqué.

Le pilote et le passager éventuel prennent place dans la nacelle qui se trouve suspendue au tore. Les déplacements sont assurés par trois systèmes de propulsion. Chaque propulseur est composé d'un quadricoptère qui embarque quatre batteries, quatre variateurs, quatre moteurs et quatre hélices.

Pour une vitesse de consigne en échelon de 600 tr·min-1, les concepteurs du projet souhaitent une erreur statique nulle et un temps de réponse à 5 % inférieur à 500 ms : ces critères correspondent au cahier des charges de cette partie.

L'objectif de cette partie est de vérifier si l'évolution de la vitesse de rotation du moteur respecte le cahier des charges.

L'action sur le joystick par le pilote permet au contrôleur de vol de calculer les consignes de vitesses à imposer à chacun des 12 moteurs. Le pilote impose une consigne de vitesse de déplacement de l'Aéronde de 25 km·h-1 correspondant à une vitesse de rotation moyenne des moteurs N0 = 600 tr·min-1.
Dans le laboratoire d'une école d'ingénieur de Grenoble, où sont réalisés les essais des propulseurs, un modèle multi-physique permet de commander les moteurs et d'ainsi vérifier la vitesse de déplacement de l'Aéronde. Ce logiciel permet aussi d'avoir l'évolution de la vitesse en temps réel.
L'objectif intermédiaire est d'identifier l'ensemble moteur plus variateur.

La simulation est lancée afin de caractériser le moteur et le relevé obtenu est fourni ci-après.

1. En considérant que cette réponse est assimilée à une réponse du 1er ordre, déterminer la valeur de la constante de temps électromécanique du moteur τ_em.

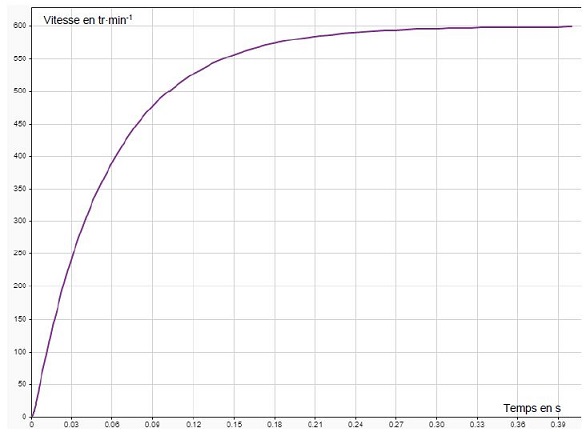
2. Pour obtenir ce relevé, la tension de commande Uc(t) = 40 V a été placée au niveau de l'entrée du modèle, en déduire la valeur du gain G de cette chaîne directe.

Le moteur étant identifié (modèle de comportement), il est décidé d'asservir sa vitesse de rotation. Cet asservissement de vitesse peut se représenter ainsi :

La simulation est lancée et les deux relevés sont obtenus pour deux valeurs du gain du correcteur.

La simulation est lancée et les deux relevés sont obtenus pour deux valeurs du gain du correcteur.

3. Indiquer la valeur du temps de réponse à 5 % pour chacun des essais.
4. Préciser ensuite la valeur de l'erreur statique relative Ε_r en vitesse (exprimée en %) pour chacun des essais.
5. Conclure sur le numéro de l'essai et donc du choix du correcteur qui satisfait aux contraintes imposées par le cahier des charges.

1. τ_em est le temps que met le système pour atteindre 63% de la consigne, soit 600*63% = 370 tr.min^-1
On peut voir sur la courbe que l'on se trouve aux alentours de 0,06s ou 60 ms.

2. Le gain du système est le rapport de la sortie sur l'entrée.
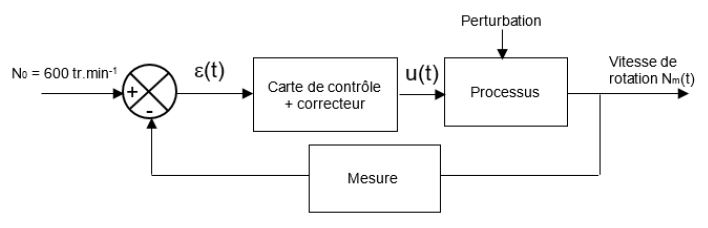
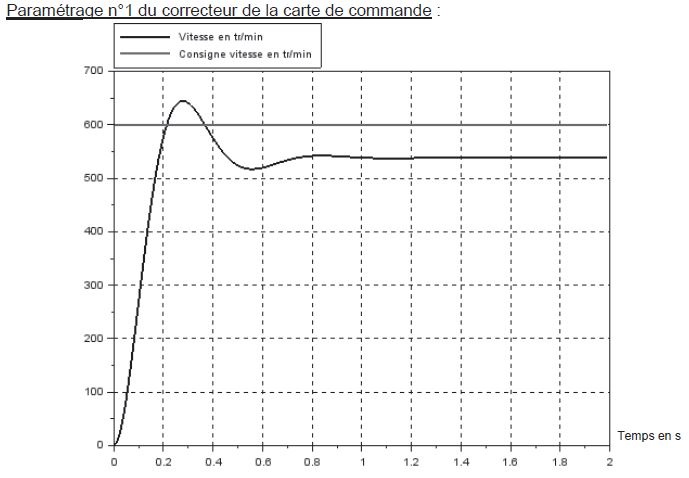
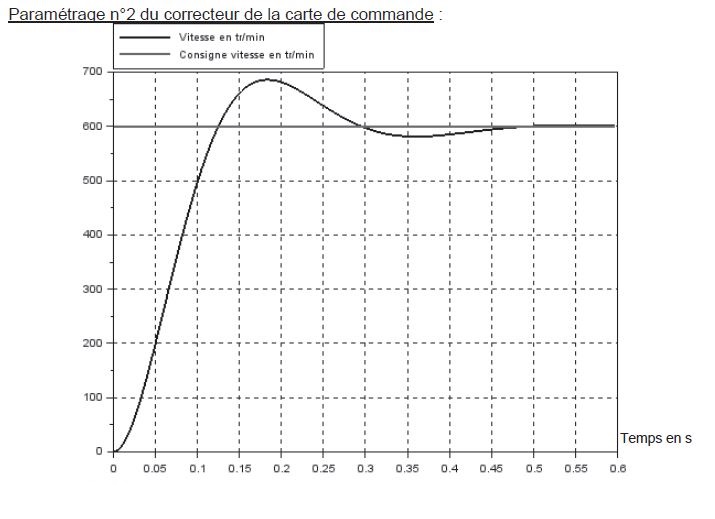
On a donc: G= ΔS / ΔE = ΔN / ΔU = 600 / 40 = 15 tr.min^-1

3. Pour le premier essai:
Sur la courbe, on voit que la valeur finale est environ de 540 tr.min^-1.
On calcule la valeur à ±5%, soit 1,05*540=567 et 0,95*540=513. On trace la droite correspondantes à ces deux valeurs sur la courbe (zone bleue claire sur la courbe) et on regarde à partir de quand la courbe reste entre ces deux valeurs.
Ici, on trouve t_r5%= 420ms.

Pour le deuxième essai: On effectue la même démarche et on trouve t_r5%= 260ms.

4. L'erreur statique est l'écart entre la valeur finale et la consigne. Elle se calcule de la façon suivante:

ε_r= consigne - valeur finale / consigne
Pour le premier essai:

ε_r= 600-540 / 600 = 0,1 soit 10%

Pour le deuxième essai:
Pour le deuxième essai, on remarque le la valeur finale est à la consigne donc l'erreur statique est nulle.

5. Les contraintes imposées par le cahier des charges est un temps de réponse à 5% t_r5% <500 ms et une erreur statique nulle.
Le deuxième essai répond le mieux au cahier des charges avec un t_r5%=260ms et une erreur statique nulle.

Retour à l'accueil

Navigation